
A função polinomial do primeiro grau mais simples é a função identidade
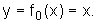
Cada ponto de seu gráfico é da forma
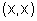 pois a ordenada y é sempre igual à abscissa x, para cada valor da variável independente x.
pois a ordenada y é sempre igual à abscissa x, para cada valor da variável independente x. Nosso objetivo é o de entender a função mais geral
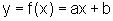 , observando que seu gráfico pode ser obtido a partir do gráfico de
, observando que seu gráfico pode ser obtido a partir do gráfico de 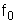 se consideramos as operações realizadas como transformações no plano. Dessa forma, ao final, teremos uma visão de qual o significado dos parâmetros a e b envolvidos na expressão da função.
se consideramos as operações realizadas como transformações no plano. Dessa forma, ao final, teremos uma visão de qual o significado dos parâmetros a e b envolvidos na expressão da função. Assim, começando pela função y = x cujo gráfico é:
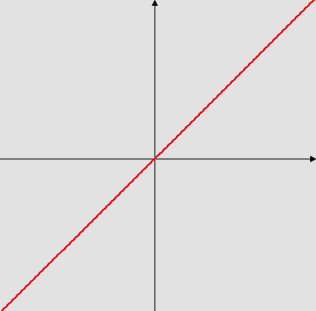
Observemos no gráfico que o ângulo, entre o eixo x e a reta resultante de y = x, mede 45o, uma vez que ela contém as bissetrizes do primeiro e do terceiro quadrantes.
 Uma função polinomial do primeiro grau um pouco mais geral tem a expressão dada por
Uma função polinomial do primeiro grau um pouco mais geral tem a expressão dada por 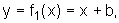 onde b é uma constante real. A pergunta natural a ser feita é: qual a ação da constante b no gráfico dessa nova função quando comparado ao gráfico da função inicial
onde b é uma constante real. A pergunta natural a ser feita é: qual a ação da constante b no gráfico dessa nova função quando comparado ao gráfico da função inicial 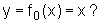
 Ainda podemos pensar numa função polinomial do primeiro grau que seja dada pela expressão
Ainda podemos pensar numa função polinomial do primeiro grau que seja dada pela expressão 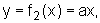 onde a é uma constante real, não nula. Novamente, a questão é investigar a ação do coeficiente a quando comparamos o gráfico de f2 ao de f0.
onde a é uma constante real, não nula. Novamente, a questão é investigar a ação do coeficiente a quando comparamos o gráfico de f2 ao de f0.  Dada
Dada 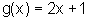 , desenhe seu gráfico, fazendo os gráficos intermediários, percebendo as ações do coeficiente 2 e depois do coeficiente 1.
, desenhe seu gráfico, fazendo os gráficos intermediários, percebendo as ações do coeficiente 2 e depois do coeficiente 1. Finalmente, podemos estudar a função polinomial do primeiro grau mais geral,
Finalmente, podemos estudar a função polinomial do primeiro grau mais geral, 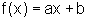 . Para tanto, interpretamos inicialmente a ação do coeficiente a da variável x e, em seguida, do termo b.
. Para tanto, interpretamos inicialmente a ação do coeficiente a da variável x e, em seguida, do termo b.Conclusão: De modo geral, conhecido o gráfico de y=x, podemos desenhar y=ax e, em seguida, y=ax+b.
Analisemos o que aconteceu:
- em primeiro lugar, em y=ax, ocorreu mudança de inclinação pois em cada ponto a ordenada é igual àquela do ponto de mesma abscissa em y=x, multiplicada pelo coeficiente a;
- em seguida, o gráfico de y=ax+b sofreu uma translação vertical de b unidades, pois, para cada abscissa, a ordenada do ponto no gráfico de y=ax+b ficou acrescida de b, quando comparada à ordenada do ponto de mesma abscissa no gráfico de y=ax.
Nomenclatura: A função polinomial do primeiro grau 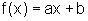 , com a não nulo, tem como domínio o conjunto R e imagem também o conjunto R, pois a variável independente x pode assumir qualquer valor e a variável dependente y=f(x) assume, em correspondência, um valor que pode ser qualquer número real.
, com a não nulo, tem como domínio o conjunto R e imagem também o conjunto R, pois a variável independente x pode assumir qualquer valor e a variável dependente y=f(x) assume, em correspondência, um valor que pode ser qualquer número real.
O coeficiente a determina a inclinação do gráfico e é denominado coeficiente angular da reta; a constante b, que determina a translação vertical do gráfico, recebe o nome de coeficiente linear da reta.
O estudo dos gráficos das funções envolvidas auxilia na resolução de equações ou inequações, pois as operações algébricas a serem realizadas adquirem um significado que é visível nos gráficos das funções esboçados no mesmo referencial cartesiano.
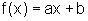 , com a não nulo, tem como domínio o conjunto R e imagem também o conjunto R, pois a variável independente x pode assumir qualquer valor e a variável dependente y=f(x) assume, em correspondência, um valor que pode ser qualquer número real.
, com a não nulo, tem como domínio o conjunto R e imagem também o conjunto R, pois a variável independente x pode assumir qualquer valor e a variável dependente y=f(x) assume, em correspondência, um valor que pode ser qualquer número real. O coeficiente a determina a inclinação do gráfico e é denominado coeficiente angular da reta; a constante b, que determina a translação vertical do gráfico, recebe o nome de coeficiente linear da reta.
O estudo dos gráficos das funções envolvidas auxilia na resolução de equações ou inequações, pois as operações algébricas a serem realizadas adquirem um significado que é visível nos gráficos das funções esboçados no mesmo referencial cartesiano.


Nenhum comentário:
Postar um comentário