Função quadrática
Origem: Wikipédia, a enciclopédia livre.
Em matemática, uma função quadrática é uma função polinomial da forma:
Se a função quadrática é igualada a zero, o resultado é uma equação quadrática. As soluções para a equação são chamadas raízes da equação ou os zeros da função, e são os interceptos do gráfico da função com o eixo x.
Índice[esconder] |
[editar] Origem da palavra
O adjetivo quadrática vem da palavra latina quadratum, que significa quadrado. Um termo como x2 é chamado de quadrado em álgebra, porque representa a área de um quadrado de lado x.Em geral, um prefixo quadr(i)- indica o número 4. Como em quadrilátero e quadrante. Quadratum é a palavra latina para quadrado por que um quadrado tem quatro lados.
[editar] Raízes
 , a função terá duas raízes.
, a função terá duas raízes.
 , a equação terá uma raiz apenas (com maior precisão, diz-se que a equação tem duas raízes iguais)
, a equação terá uma raiz apenas (com maior precisão, diz-se que a equação tem duas raízes iguais)
 , não terá raíz (com maior precisão, diz-se que a equação não tem raíz reais, tendo duas raízes complexos conjugados).
, não terá raíz (com maior precisão, diz-se que a equação não tem raíz reais, tendo duas raízes complexos conjugados).
As duas raízes da equação quadrática
 , onde
, onde 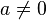 são
são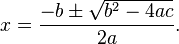
Essa fórmula é chamada de Fórmula de Bhaskara.
- Dado

- Se
 , então existem duas raízes distintas uma vez que
, então existem duas raízes distintas uma vez que 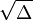 é um número real positivo.
é um número real positivo. - Se
 , então as duas raízes são iguais, uma vez que
, então as duas raízes são iguais, uma vez que 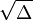 é igual a zero.
é igual a zero. - Se
 , então as duas raízes são números complexos conjugados, uma vez que
, então as duas raízes são números complexos conjugados, uma vez que 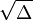 é imaginário.
é imaginário.
 e
e  ou vice versa, é possível fatorar
ou vice versa, é possível fatorar  como
como  .
.[editar] Concavidade do gráfico da função quadrática
A concavidade é a abertura da parábola, que ora está voltada para cima e ora está voltada para baixo. O sentido da concavidade depende do coeficiente a, se este for superior a 0, ou seja, positivo, ela é voltada para cima, caso seja negativo ela é voltada para baixo.[editar] Vértice da parábola
O vértice da parábola corresponde ao ponto mais extremo dela. É definido pelas seguintes coordenadas: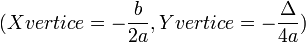
[editar] Crescimento e decrescimento de uma função quadrática
Em uma parábola, metade é crescente e a outra metade é decrescente.- Concavidade voltada para cima:
- Decrescente do -infinito ao vértice
- Crescente do vértice ao infinito
- Concavidade voltada para baixo:
- Crescente do -infinito ao vértice
- Decrescente do vértice ao infinito
[editar] Formas da função quadrática
Uma função quadrática pode ser expressa em três formatos: é chamada a forma geral ou forma polinomial (também chamada de forma desenvolvida),
é chamada a forma geral ou forma polinomial (também chamada de forma desenvolvida),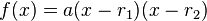 é chamada a forma fatorada, onde r1 e r2 são as raízes da equação quadrática, e
é chamada a forma fatorada, onde r1 e r2 são as raízes da equação quadrática, e é chamada a forma padrão ou forma vértice (também chamada de forma canônica).
é chamada a forma padrão ou forma vértice (também chamada de forma canônica).
[editar] Gráfico
Independentemente do formato, o gráfico de uma função quadrática é uma parábola (como mostrado abaixo).- Se
 , a parábola abre para cima.
, a parábola abre para cima. - Se
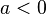 , a parábola abre para baixo.
, a parábola abre para baixo.
O coeficiente b e a, juntos, controlam o eixo de simetria da parábola (e também a coordenada do x do vértice).
O coeficiente b sozinho é a declividade da parábola ao cortar o eixo y.
O coeficiente c controla a altura da parábola, mais especificamente, é o ponto onde a parábola corta o eixo y.
[editar] Vértice
O vértice de uma parábola é o número crítico da função quadrática - o ponto onde ela vira, também chamado de turning point. Se a função estiver na forma padrão, o vértice é dado por . Pelo método de completar o quadrado transforma-se a forma geral:
. Pelo método de completar o quadrado transforma-se a forma geral: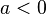 ou o ponto mínimo se:
ou o ponto mínimo se: .
.
- Pontos de máximo/mínimo
- O máximo ou mínimo de uma função é sempre obtido no vértice. O seguinte método se baseia na mesma idéia fazendo uso do cálculo. A vantagem desse método é que ele funciona para funções mais gerais.
- Tomando
 como um exemplo de equação quadrática para achar seus pontos extremos (que dependem de
como um exemplo de equação quadrática para achar seus pontos extremos (que dependem de  , se
, se  , tem um ponto mínimo, se
, tem um ponto mínimo, se 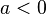 , tem um ponto máximo) é necessário antes encontrar sua derivada:
, tem um ponto máximo) é necessário antes encontrar sua derivada:
- Depois, encontramos as raízes de
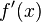 :
:
- Então,
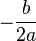 é o
é o  valor de
valor de 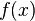 . Agora, para encontrar o valor de
. Agora, para encontrar o valor de 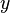 , substituimos
, substituimos 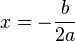 em
em 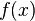 :
:
- Assim, as coordenadas do ponto mínimo/máximo são:
[editar] Estudo dos Sinais
O estudo dos sinais da função quadrática define os sinais da função para qualquer valor de x. O estudo depende do sinal do coeficiente a e do Δ. Ele é obtido analisando o esboço do gráfico da concavidade da função.[editar] - 1º Caso: Δ < 0
Neste caso, a parábola da função não corta o eixo das absissas. Portanto: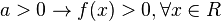
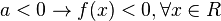
[editar] - 2º Caso: Δ = 0
Neste caso, a parábola da função corta o eixo das absissas em apenas um ponto. Tem-se duas situações, dependendo o valor do coeficiente a e das raízes r1 e r2 (note que r1 < r2):- a > 0

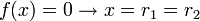
- a < 0
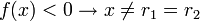
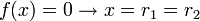
[editar] - 3º Caso: Δ > 0
Neste caso, a parábola da função corta o eixo das absissas em dois pontos. Novamente, tem-se duas situações, dependendo o valor do coeficiente a (note novamente que r1 < r2):
- a > 0


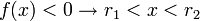
- a < 0
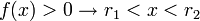

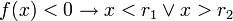
[editar] Raiz quadrada de uma função quadrática
A raiz quadrada de uma função quadrática faz surgir ou uma elipse ou uma hipérbole. Se então a equação
então a equação  descreve uma hipérbole. O eixo da hipérbole é determinado pela ordenada do ponto mínimo da parábola correspondente
descreve uma hipérbole. O eixo da hipérbole é determinado pela ordenada do ponto mínimo da parábola correspondente 
Se a ordenada for negativa, então o eixo da hipérbole é horizontal. Se ordenada for positiva, então o eixo da hipérbole é vertical.
Se
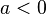 então a equação
então a equação  descreve ou uma elipse ou absolutamente nada. Se a ordenada do ponto máximo da parábola correspondente
descreve ou uma elipse ou absolutamente nada. Se a ordenada do ponto máximo da parábola correspondente  for positiva, então sua raiz quadrada descreve uma elipse, mas a ordenada for negativa ela descreve um conjunto vazio de pontos.
for positiva, então sua raiz quadrada descreve uma elipse, mas a ordenada for negativa ela descreve um conjunto vazio de pontos.[editar] Função quadrática bivariada
Uma função quadrática bivariada é um polinômio de segundo grau da forma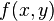 igual a zero, é descrita a intersecção da superfície com o plano
igual a zero, é descrita a intersecção da superfície com o plano  , que é um locus de pontos equivalente a uma secção cônica.
, que é um locus de pontos equivalente a uma secção cônica.[editar] Mínimo/máximo
Se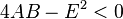 a função não possui máximo ou mínimo e seu gráfico forma um parabolóide hiperbólico.
a função não possui máximo ou mínimo e seu gráfico forma um parabolóide hiperbólico.Se
 a função possui um mínimo se A>0, e um máximo se A<0 e seu gráfico forma um parabolóide elíptico.
a função possui um mínimo se A>0, e um máximo se A<0 e seu gráfico forma um parabolóide elíptico.O mínimo ou máximo de uma função quadrática bivariada é obtido através de
 onde:
onde: e
e  a função não possui máximo ou mínimo e seu gráfico forma um cilindro parabólico.
a função não possui máximo ou mínimo e seu gráfico forma um cilindro parabólico.Se
 e
e 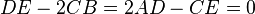 a função alcança o mínimo/máximo em uma linha. Similarmente, um mínimo se A>0 e um máximo se A<0, e seu gráfico forma um cilindro parabólico.
a função alcança o mínimo/máximo em uma linha. Similarmente, um mínimo se A>0 e um máximo se A<0, e seu gráfico forma um cilindro parabólico.[editar] Ver também
- Forma quadrática
- Representação matricial de secções cônicas
- Quádrica
- Pontos periódicos de mapeamentos quadráticos complexos
[editar] Ligações externas
- Quadratic em MathWorld. ((en))



 Ver artigo principal:
Ver artigo principal: 

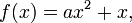


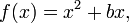



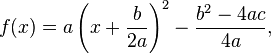








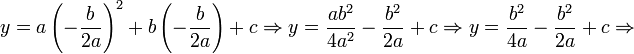
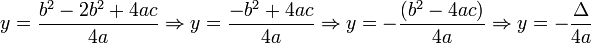


 e nula para
e nula para 



Nenhum comentário:
Postar um comentário