H

História da Matemática




Pitágoras de Samos
Pitágoras de Samos, 590 – 495 a.C.
Pitágoras de Samos viveu no período entre 580 ou 590 e 500 a.C. e é geralmente considerado um dos maiores professores gregos desta época mais remota. Pitágoras foi um importante contemporâneo de Thales (de Miletus).
Outra linha de pensamento da Grécia antiga foi a Escola Pitágorica. Desenvolveu-se numa colônia grega no sul da península Itálica, supostamente liderada pelo legendário Pitágoras. Os números eram classificados com critérios peculiares como: pares e ímpares, primários e secundários, perfeitos e imperfeitos, quadrados, poligonais, etc. Estudaram de forma geométrica algumas séries numéricas como a dos “números triangulares’’”.

Mapa da Escola Pitagórica
No que concerne à estrutura do Universo, acreditavam ser inteiramente regido por “harmonia e número'', concebido como foi por um D-us geômetra. O Universo seria dotado de um “fogo central’’ ao redor do qual girariam a Terra, a Lua, o Sol, os planetas e as estrelas”. Tendo constatado a existência de relações numéricas entre os comprimentos das cordas de instrumentos musicais capazes de produzir harmonia musical, acreditavam que tais números encerrariam certa harmonia mais fundamental que regeria a ordem do Universo, “a Música das Esferas”. As distâncias dos diversos corpos celestes ao fogo central estariam de acordo com os intervalos musicais produzindo um gigantesco acorde. Este acorde não seria, no entanto audível ao ouvido humano. Se certos detalhes da concepção pitágorica do mundo podem nos parecer ingênuos, a crença na existência de uma ordem matemática subjacente à natureza é essencial à Física e está implícita na busca de modelos e equações gerais da natureza.

Cosmogonia de Pitágoras
Ele fundou uma escola que misturava Filosofia natural e misticismo e que atraiu muitos seguidores. Vários estudiosos preferem dizer que Pitágoras formou um culto e não uma escola em Crotona, sul da Itália. Por que um culto? Os seguidores de Pitágoras viviam em um rígido regime, que incluía o vegetarianismo, os votos de silêncio durante os cinco primeiros anos de permanência no grupo, e total anonimato em relação a feitos pessoais.
 “Tinha o caráter de um movimento religioso, uma peculiar religião onde a geometria e a
“Tinha o caráter de um movimento religioso, uma peculiar religião onde a geometria e a matemática possuíam um papel privilegiado. Pregava esta escola que durante a vida
humana o corpo vivo seria a ‘tumba da alma’, que renasceria por ocasião de sua morte”.
Sua doutrina previa uma série de práticas ascéticas destinadas a manter a alma livre da contaminação ocasionada por sua “prisão durante a vida”. Os números e figuras geométricas possuiriam poderes especiais, sendo o próprio Criador do Universo um geômetra. A atividade desta escola ultrapassou o pensamento religioso: atribuem-se a ela diversos, tendo chegado também à maioria das conclusões expressas mais tarde nos Elementos de Euclides.
Devido a estas restrições é difícil saber o que foi feito por Pitágoras e o que foi feito pelos seus seguidores.
A escola de Pitágoras fez vários desenvolvimentos na matemática. Foram seus seguidores que, pela primeira vez, reconheceram a existência de números irracionais. No entanto, havia também um pouco de misticismo nos seus estudos. Para os pitagóricos o ponto estava associado ao número 1, uma linha com o número 2, uma superfície com o 3 e um sólido com o 4. Sua soma dava 10, número então considerado sagrado e onipotente.

Números Perfeitos
Pitágoras é mais conhecido pelo seu teorema, o Teorema de Pitágoras:

Teorema de Pitágoras
 "Em um triângulo retângulo o comprimento da hipotenusa elevado ao quadrado é igual à
"Em um triângulo retângulo o comprimento da hipotenusa elevado ao quadrado é igual à soma dos comprimentos de cada cateto elevado ao quadrado."
(Pitágoras)
O teorema de Pitágoras já era conhecido pelos antigos babilônios, mas parece que Pitágoras foi o primeiro a demonstrá-lo. Os desenvolvimentos feitos na astronomia pelos membros da escola de Pitágoras estavam baseados nos estudos de Anaximander. Parece que o conceito de "movimento circular perfeito" veio de Anaximandro.
A escola de Pitágoras estava interessada na relação entre a música e a matemática. Eles provaram que os intervalos musicais seguem proporções numéricas. Seus membros acreditavam que os planetas estavam associados a esferas cristalinas, uma para cada planeta, as quais produziam a "Música das Esferas". Estas esferas estavam centradas na Terra, e ela mesma estava em movimento. Nós não notamos a "música das esferas" porque ela sempre esteve à nossa volta e, portanto, não sabemos como seria não sentir o seu som.
É provável que Pitágoras tenha sido o primeiro a supor que a Terra é uma esfera. Alguns também atribuem a Pitágoras ter reconhecido que a "estrela matutina" e a "estrela vespertina" são ambas, o planeta Vênus.
Embora somente oito corpos celestes fossem conhecidos naquela época, Pitágoras acreditava que deveria haver dez - os cinco planetas conhecidos, o Sol, a Lua, a Terra, e uma chamada "contra Terra" designada pelo termo grego “antikhthon”.
Escola Pitagórica ou Itálica , 590 - 495 a.C.

Magna Grécia - Escola Itálica ou Pitagórica
Depois da Escola Jônica fundada por Tales de Mileto a qual deu origem à Filosofia grega, segue cronologicamente, pela ordem de antiguidade, a Escola Itálica ou Pitagórica, fundada por Pitágoras, natural de Samos, em 590/495 a.C. Ele sofreu perseguição política devido suas idéias, deixando sua terra, instalou-se em Crotona, sul da Itália, região conhecida como Magna Grécia, fundou ali uma sociedade filosófica que exerceu grande influência política.
Para ele as essências de todas as coisas residiam nos números, os quais representam a ordem e a harmonia. As contribuições da Escola Pitagórica podem ser encontradas no campo da matemática (Teorema de Pitágoras), música e astronomia. A essas contribuições juntam-se uma série de crenças místicas relativas à imortalidade da alma, às reencarnações dos pecadores, à prescrição de rígidas condutas morais, etc. Ele afirma que a verdadeira substância original é a alma imortal, que preexiste ao corpo e no qual se encarna como em uma prisão, como castigo pelas culpas da existência anterior.
O problema da arché ou do principio também faz parte da Escola Itálica ou Pitagórica, bem como, tinha em sua essência uma orientação bem diversificada. Provavelmente nada tenha sido escrito por Pitágoras, sua escola se organizou em estilo de congregação político-religiosa.
Tudo se baseia no número, na forma, na harmonia das esferas.
 Célebres pitagóricos foram:
Célebres pitagóricos foram:  Filolao de Crotona;
Filolao de Crotona;  Timeu de locre;
Timeu de locre; Arquita de tarento;
Arquita de tarento; Ocelos da Lucânia;
Ocelos da Lucânia; Símias;
Símias; Cebes;
Cebes; Lísis, o mestre de Epaminondas.
Lísis, o mestre de Epaminondas.Para Pitágoras o número é o principio de tudo (arché), dele todas as coisas derivam e são compostas.
Quem é D-us para Pitágoras?
 "D-us é a grande Unidade, a Mônada, o número perfeito do qual emanam todos os outros
"D-us é a grande Unidade, a Mônada, o número perfeito do qual emanam todos os outros seres do mundo”.
(Pitágoras).
A Escola Itálica ou Pitagórica se diferencia da Escola Jônica. À Escola de Eléia ou Jônica é que cabe o mérito, senão de ter fundado a Metafísica, pelo menos de ter elevado o pensamento grego ao nível próprio da Metafísica e ao grau de abstração que comporta esta ciência. A Escola Itálica é mais baseada na ordem que preside o cosmos (termo criado por Pitágoras), assim sendo, melhor se apresenta com o nome de Escola Pitagórica, até mesmo porque depois se difundiu pelo mundo conhecido como helênico, o pitagorismo se destacou pelo seu racionalismo, em contraste com a moderação da Escola Jônica.
Sempre ficou muito claro que a razão caminha mais longe do que o sentido, delimitado pelo superficialismo dos objetos. Os sentidos têm como objeto as qualidades sensíveis, em função das quais se pensa haver a matéria sensível, e não é, ou simplesmente dizendo, sim e não.
Argumenta-se até onde vai este conhecimento racional da mente? Os Empiristas e Racionalistas discordam sobre esta dimensão do pensamento. Em cada caso as discordâncias são, ora mais radicais, ora menos. Há um empirismo que permanece apenas no sentido; este é o sensismo, o qual reduz o pensamento apenas em uma sensação pouco utilizada. E há um empirismo, e este é o mais freqüente, que admite a especificidade do pensamento. Todavia este empirismo atribui valor ao pensamento enquanto aprende os objetos da experiência.
O modelo astronômico interessante foi sugerido por volta de 410 a.C. pelo filósofo Filolau (de Crotona) que postulou que o fogo central no universo, chamado "Héstia", e que alguns pitagóricos colocavam no centro da Terra, na verdade marcava o centro do universo.

Universo - Modelo de Filolau
Ao adotarem o modelo de Filolau, os seguidores de Pitágoras, no século V a.C., passaram a acreditar que nem a Terra nem o Sol, mas sim um "fogo central", estava no centro do universo. Isso fazia com que a Terra fosse deslocada para fora do centro do universo, e agora passasse a circular em torno da Héstia.
Os pitagóricos colocaram esse fogo no "centro escondido das coisas". Era esse fogo que fornecia a energia para que os corpos celestes pudessem se movimentar. Em torno deste "fogo central" moviam-se os planetas conhecidos, a Terra, a contra-Terra, a Lua e o Sol, cada um deles associado à sua própria esfera de cristal. A Terra girava mais próxima do "fogo central" do que qualquer um dos outros corpos visíveis no céu. A Terra estava protegida deste "fogo central" pela "contra-terra", razão pela qual nós não víamos o fogo central: a “contra-Terra” que circulava em volta da “Héstia”, bloquearia a sua visão para os terráqueos. Uma outra razão pela qual nunca vemos ou somos torrados por esse fogo é pelo fato de que vivemos sobre somente metade da esfera da Terra e essa nossa metade está sempre virada na direção contrária ao fogo. Isso torna necessário que a Terra gire em torno do seu eixo à medida que percorre sua órbita, uma revolução completa por órbita exatamente como a lua percorre sua órbita em torno da Terra mostrando sempre a mesma face. Para os pitagóricos esta rotação da Terra em torno do seu eixo explica (corretamente) o modelo de dia e noite.
Acredita-se que a "contra-Terra" foi "inventada" para explicar os eclipses, em particular porque os eclipses lunares são mais freqüentes do que os solares, mas também para fazer com que o número de objetos que circundavam o fogo central fosse 10, o número mágico dos pitagóricos.
Deste modo os pitagóricos foram os primeiros a produzir uma teoria astronômica na qual uma Terra esférica girava em torno de seu próprio eixo assim como se movia em uma órbita. Note que essa teoria surgiu em parte devido à necessidade de localizar o grande fogo que eles acreditavam alimentar o universo.
Como exemplo da doutrina mística pitagórica acerca do homem, podem-se tomar alguns fragmentos ou doxografias de “Álcmeão de Cróton”, que pertencia à escola ou pelo menos em estreita relação com ela, e que, no dizer de Aristóteles, era ainda jovem quando Pitágoras já entrara em sua velhice. O significado de Alcmeão, como é bem sabido, reside principalmente em suas investigações fisiológicas, médicas e psicológicas.
 "Álcmeão diz que (a alma) é imortal por parecer-se às coisas imortais, e isto é assim por
"Álcmeão diz que (a alma) é imortal por parecer-se às coisas imortais, e isto é assim por estar sempre em movimento; pois todas as coisas divinas movem-se sempre
continuamente: a Lua, o Sol, os astros e todo o céu."
(Aristóteles, De Anima, I, 2.).
 "Alcmeão afirma que o homem se distingue dos demais “entes” porque só ele pensa,
"Alcmeão afirma que o homem se distingue dos demais “entes” porque só ele pensa, enquanto os demais “entes” têm sensação, mas não pensam."
(Teofrasto, Das sensações 25.)
Aparecem claramente assinalados três momentos importantes: em primeiro lugar, a distinção entre o corpo e a alma; em segundo lugar, a diferença entre o homem e o animal, reconhecida em sua faculdade pensante; em terceiro lugar, a relação com os deuses e o problema da imortalidade. A alma humana é imortal por sua relação com as coisas divinas, às quais se assemelha por seu eterno movimento; esta teoria terá repercussões em Platão (cf. Fedro, 245 e ss.); mas, por outro lado, cabe ao homem certa mortalidade por não possuir o movimento perfeito, circular, dos astros divinos, que simboliza a eternidade por sua união do princípio com o fim. Encontramos já, neste pitagórico, os pontos capitais que a especulação helênica acerca do homem irá abordar.
Xenófanes de Cólofon, 570 - 475 a.C.

Xenófanes de Cólofon
Era filho de Déxio (ou Ortomenes) e nasceu em Cólofon, na Jônia, por volta de 570; quando contava com cerca de 25 anos, teve de emigrar devido à invasão persa. Sem residência fixa, levou uma vida errante. Passou parte dela na Sicília. Foi poeta, sábio e cantou seus poemas através da Grécia. Em oposição aos Filósofos de Mileto, só escreveu em versos. Visitou então várias cidades da Sicília e é possível que tenha estado também em Eléia. Teve vida longa e faleceu por volta de 475 com mais de noventa anos.
Sua principal atividade era, aparentemente, a poesia, mas alguns de seus poemas têm importante conteúdo filosófico. Ao contrário dos milesianos, escrevia sempre em versos, dos quais nos restam diversos fragmentos. Xenófanes, aliás, é o primeiro dos Filósofos pré-socráticos de quem temos quantidade considerável de fragmentos (quarenta e um).
Xenófanes escreveu em versos sua oposição às idéias de Tales, Anaximander, Anaximandro e Anaxímenes. Chegaram até nós diversos de seus versos e de suas idéias Filosóficas. Delas podemos destacar seu combate ao antropomorfismo (atribuir aos deuses formas e sentimentos humanos) que ele expressa especialmente contra os poemas de Homero e Hesíodo. Ele dizia que se os animais tivessem o dom da pintura eles iriam pintar seus deuses com formas animais.
 "Mas se os bois, os cavalos e os leões tivessem mãos ou se fossem capazes como os
"Mas se os bois, os cavalos e os leões tivessem mãos ou se fossem capazes como os homens de pintar obras com as mãos, os cavalos como os cavalos, os bois como os bois
pintariam o aspecto dos deuses, e fariam o corpo deles tal qual cada um deles o tem."
(Frag. 15).
 "Homero e Hesíodo atribuíram aos deuses tudo aquilo que para os homens é objeto de
"Homero e Hesíodo atribuíram aos deuses tudo aquilo que para os homens é objeto de vergonha e baixeza: roubar, praticar adultério e enganar-se... Os mortais consideram
que os deuses nasceram, e que possuem roupas, vozes e corpos como os seus... Os
Etíopes acreditam que seus deuses possuem narizes achatados e que são negros; e os
trácios que os seus deuses possuem olhos azuis e cabelo vermelho... mas se os bois,
cavalos e leões tivessem mãos e soubessem desenhar... os cavalos desenhariam figuras
de deuses semelhantes a cavalos, os bois semelhantes a bois."
Ele queria com isso mostrar que o verdadeiro Deus é único, absoluto e tem pouca semelhança com os homens, com seus pensamentos ou com as diversas representações feitas dele. Esse deus único é diretamente ligado ao cosmos, ele tudo vê, pensa e ouve e com a força do seu pensamento faz tudo vibrar, ele está sempre no mesmo lugar e não se move, pois não é próprio de um deus estar hora em um lugar e depois noutro.

Homero
Ficou famoso com estes ataques aos poetas Hesíodo e Homero e aos pensadores Tales, Pitágoras e Epimênides. Nos fragmentos 173 a 175, Xenófanes afirmou a existência de um só Deus, sem forma e pensamento humanos, imóvel e onipotente, mostrando que suas desconfianças lançadas sobre os mitos não visavam extinguir o pensamento religioso, ou a forma mítica em si, mas tão somente a falta de propriedade desse tipo de narrativa em abordar questões religiosas, morais ou, por extensão, tudo aquilo que fosse passível de ser contradito por um discurso "verdadeiro".
Com sua filosofia panteísta, dedicou-se a demonstrar a unidade e perfeição de Deus e exerceu influência sobre a escola filosófica da cidade de Eléia, nos séculos posteriores, que se tornaria célebre por grandes filósofos como Parmênides e Zenão.
Xenófanes era de Colofão, mas viajou por diversos lugares das colônias gregas itálicas. Ele recitava seus poemas como um Filósofo andarilho, além de criticar o antropomorfismo ele defendia a sabedoria e os prazeres vividos socialmente, mas sem excessos. Ele era um pensador independente e acreditava que da terra é que surgiam as coisas. A terra é o princípio das coisas que são feitas de terra e água, inclusive o homem.
Moralmente o filósofo destaca como superiores os valores da inteligência e da sabedoria sobre os valores da força física, que era muito valorizada pelos gregos da época e tinha no atleta o seu representante. Para Xenófanes o que torna melhor os homens e as cidades “pólis” em que eles vivem é à força da inteligência e da sabedoria. Tudo vem da terra e para ela volta.
Embora Aristóteles tenha atribuído a ele a fundação da Escola Eleática de Filosofia, representada por Parmênides, Zênon e Melisso, não há dados seguros que apóiem essa afirmação. O pensamento de Xenófanes, além disso, tem semelhanças muito superficiais com o dos eleatas.
A importância de Xenófanes para a Filosofia reside principalmente no espírito crítico e no ceticismo com que encarava o antropomorfismo e moralidade das divindades gregas, e também as limitações do conhecimento humano. Através de seus versos criticou asperamente o hábito humano de representar as divindades à sua própria semelhança e foi, também, o primeiro Filósofo grego a postular a possível existência de um deus único.
 FRAGMENTOS, EDIÇÕES E TRADUÇÕES.
FRAGMENTOS, EDIÇÕES E TRADUÇÕES.
A fonte dos fragmentos de Xenófanes é muito variada, mas a maior parte vem de Ateneu, séc. II/III, Diógenes Laércio, 200/250; e Clemente de Alexandria, 150/215.
Fragmentos de Henri Estienne “Henricus Stephanus”, publicada em 1573. Depois vieram as coletâneas de Brandis “1813”; Karsten “1835”; Mulach “1845”; Bergk “1878/1882”; Wachsmuth “1885”. Mais recentemente, Diehl “1949”; West “1972”, editaram os fragmentos poéticos e Diels-Kranz “1951, os Filosóficos. Das edições recentes, a de Gentili e Prato “1988”, é uma das mais usadas.
Escola Eleática, 570 -

Mapa de localização da Escola Eleática
A Escola Eleática de Filósofos foi a quarta das antigas escolas filosóficas gregas. Ela foi fundada pelo poeta e pensador religioso Xenófane (nascido por volta de 570 a.C.). Seu principal ensinamento era que o universo é singular, eterno e inalterável. Segundo Xenófane "O todo é um".
A Escola Eleática se opunha à doutrina jônica de desenvolvimento.
Os eleáticos viam a natureza como uma unidade imutável, universal, considerando a criação, a variedade, a mudança e o movimento como ilusões dos sentidos. Para eles toda mutação é ilusória e as transformações observadas na natureza são pura ilusão dos sentidos.
O maior dos filósofos eleáticos foi Parmênides (nascido por volta de 539 a.C.). Acredita-se que ele foi quem introduziu o argumento lógico na Filosofia.

Parmênides de Eléia
Parmênides tinha como hábito acompanhar cada uma de suas afirmações com algum tipo de argumento lógico que justificava o “por que do fato”, narrado ocorrer daquela maneira.
As crenças de Parmênides na unidade absoluta e constância da realidade são bastante radicais e abstratas, mesmo para os padrões modernos.
Um dos estudantes de Parmênides foi Zenon de Elea, 490 - 425 a.C.. Ele é lembrado por ter usado uma série de argumentos nos quais defende a Filosofia eleática pondo a prova, por meios lógicos, que a mudança (movimento) e a pluralidade são impossíveis.
Nenhum dos escritos de Zenon sobreviveu e só sabemos sobre suas idéias a partir dos textos de Platão, Aristóteles, Simplício e Prócro, que não são simpáticos ao que ele defendia. A principal fonte do nosso conhecimento sobre as idéias de Zenon está no diálogo "Parmênides" escrito por Platão.
Zenon escreveu um livro que continha 40 paradoxos que dizem respeito ao “continuum”. Quatro destes paradoxos tiveram uma profunda influência no desenvolvimento da matemática: a "dicotomia", "Aquiles e a tartaruga", "a flecha" e o "stadium".


A Dicotomia

A Tartaruga

A Flecha


O Stadium
O mais conhecido desses paradoxos é aquele intitulado "Aquiles e a Tartaruga" no qual ele levanta a questão de que "o mais lento nunca será superado pelo mais rápido pois aquele que está indo no encalço do outro deve primeiro alcançar o ponto a partir do qual aquele que está fugindo partiu, de modo que o mais lento deve sempre estar alguma distância a frente do mais rápido".
É na Itália meridional que floresce a terceira escola, e o idealismo absoluto, fora do que é real, seu fundador é o poeta Xenófane, crítico das duas escolas anteriores, para ele só a inteligência pode chegar a compreender o princípio fundamental da vida, ridicularizou a metempsicose de Pitágoras. A escola eleática negou o politeísmo e criou o monoteísmo, Parmênides e Zenon continuaram a obra de Xenófane, para eles não há nascimento nem morte, tudo é eterno e imperecível, os sentidos nos enganam: tudo é aparência, por trás das aparências está a realidade.
Os sofistas rejeitam o absoluto dos eleatas, desprezam o testemunho dos sentidos, preparam o futuro do subjetivismo. Notáveis sofistas foram: Górgias e Hípias, Protágoras e Pródico, entre os sofistas, Zenon negava o movimento, resposta de Diógenes foi andar.
Protágoras por haver negado a existência dos deuses foi condenado como ímpio e seus livros queimados em praça pública, morreu quando fugia. Restaram: Metrodoro de quios, Diomenes de smirna, Anaxarque de Abdera.
Álcmeon de Crotona, 520 – 450 a.C.

Álcmeon de Cróton
Álcmeon de Crotona (c. 520 – c. 450 a.C.) foi um dos principais discípulos de Pitágoras e de primeira hora. Floresceu quando o mestre já estava idoso, e portanto na volta dos anos 400 a.C. Não é o mesmo Álcmeon, filho de Anfiaro, citado por Ovídio.
Havendo estudado a natureza como físico e como médico, foi talvez o primeiro a praticar a pesquisa pela dissecação dos corpos e a aventurar-se a fazer uma operação nos olhos. Infere de suas experiências, que no cérebro está a sede do pensamento.
Muito pouco resta de suas obras e poucas são as informações doxográficas. Praticou a medicina, a física, bem como a filosofia em geral, advertindo para a doutrina dos contrários, típicas do pitagorismo, as quais, todavia têm origem, em última instância no orfismo de procedência oriental.
Tais notícias chegaram através de Diógenes Laércio. Álcmeon de Crotona outro discípulo de Pitágoras. Havendo cultivado a medicina, abordou algumas vezes a física, como quando diz, por exemplo:
 "A maior parte das coisas humanas são duplas".
"A maior parte das coisas humanas são duplas". (Alcmeon de Crotona).
Parece continua “Diógenes Laércio” como diz Favorino, em “Histórias diversas”, que foi o primeiro a escrever um Tratado sobre a Natureza, e ensinava que a natureza da Lua deve permanecer eternamente igual a que tem atualmente.
Ele é filho de Pirito, como ele mesmo diz no começo de sua obra: Alcmeon de Crotona, filho de Pirito a Brontino, Leonte e Batilo.
 "Os deuses têm um conhecimento perfeito dos segredos da natureza e de tudo que é
"Os deuses têm um conhecimento perfeito dos segredos da natureza e de tudo que é mortal. Os homens somente podem fazer conjeturas, assim por diante." (Frag. 1).
Ele disse também que a alma é imortal e que se movia sem cessar como o Sol.
 "Álcmeon de Crotona, filho de Perito, foi quem primeiro escreveu sobre a natureza.
"Álcmeon de Crotona, filho de Perito, foi quem primeiro escreveu sobre a natureza. Outros dizem que o primeiro autor do livro foi Anaxágoras de Clazômene"
(Clemente de Alexandria, Stromata, I, 78).
O caráter pitagórico de Álcmeon se manifesta na doutrina dos contrários. Ainda que não tenha conduzido a estes as características precisas, como farão os pitagóricos ulteriores, a importância está na antiguidade destes seus pontos de vista. Dos pitagóricos tomou a doutrina dos opostos (bom e mau doce e amargo, etc.) ou inversamente dele a tomaram os pitagóricos.
Aristóteles, depois de expor esta doutrina dos contrários em nome dos pitagóricos, declara:
 "Sensivelmente a mesma parece à doutrina de Álcmeon, seja porque este as recebeu dos
"Sensivelmente a mesma parece à doutrina de Álcmeon, seja porque este as recebeu dos pitagóricos, ou estes últimos, de Álcmeon, porque ele floresceu ao tempo da velhice de
Pitágoras, e as doutrinas que professaram são quase idênticas".
(Arist., Metaf., 986a 28).
No contexto pitagórico Álcmeon definiu a saúde como o equilíbrio dos contrários, e a supremacia de um dos dois a causa da doença, frag. 4..
Comentou ainda Aristóteles a respeito de Álcmeon:
 "Ele diz, com efeito, que a maior parte das coisas humanas vai a dois, designando
"Ele diz, com efeito, que a maior parte das coisas humanas vai a dois, designando contrários, tomados ao azar, e não contrários definidos como aqueles dos pitagóricos,
por exemplo, o branco e o preto, o doce e o amargo, o bem e o mal, o grande e o
pequeno. Assim, pois, este Filósofo emitiu idéias imprecisas sobre o resto, sobre os
números e contrários, enquanto que os pitagóricos explicaram claramente os números e
os contrários".
(Met., 986a 30-32).
Sobre o homem disse ainda Álcmeon:
 "Os homens morrem, porque não podem unir o princípio ao fim"
"Os homens morrem, porque não podem unir o princípio ao fim" (Frag. 2).
 "O homem distingue-se dos demais [seres] por ser o único que compreende, pois todos
"O homem distingue-se dos demais [seres] por ser o único que compreende, pois todos os outros percebem, mas não compreendem”
(Frag. 2a).
 "Mais fácil é proteger-se de um homem inimigo, do que de um amigo".
"Mais fácil é proteger-se de um homem inimigo, do que de um amigo". (Frag. 5).

Teorema de Pitágoras
Origem: Wikipédia, a enciclopédia livre.

O teorema de Pitágoras: a soma das áreas dos quadrados construídos sobre os catetos (a e b) equivale à área do quadrado construído sobre a hipotenusa (c).
| “ | Em qualquer triângulo retângulo, o quadrado do comprimento da hipotenusa é igual à soma dos quadrados dos comprimentos dos catetos. | ” |
| “ | Em qualquer triângulo retângulo, a área do quadrado cujo lado é a hipotenusa é igual à soma das áreas dos quadrados cujos lados são os catetos. | ” |
O teorema de Pitágoras leva o nome do matemático grego Pitágoras (570 a.C. – 495 a.C.), que tradicionalmente é creditado pela sua descoberta e demonstração,[1][2] embora seja frequentemente argumentado que o conhecimento do teorema seja anterior a ele (há muitas evidências de que matemáticos babilônicos conheciam algoritmos para calcular os lados em casos específicos, mas não se sabe se conheciam um algoritmo tão geral quanto o teorema de Pitágoras).[3] [4] [5]
O teorema de Pitágoras é um caso particular da lei dos cossenos, do matemático persa Ghiyath al-Kashi (1380 – 1429), que permite o cálculo do comprimento do terceiro lado de qualquer triângulo, dados os comprimentos de dois lados e a medida de algum dos três ângulos.
Índice[esconder] |
[editar] Fórmula e corolários
Sendo c o comprimento da hipotenusa e a e b os comprimentos dos outros dois lados, o teorema pode ser expresso por meio da seguinte equação: ,
,  e
e 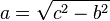 .
.| “ | Em qualquer triângulo retângulo, a hipotenusa é maior que qualquer um dos catetos, mas menor que a soma deles. [6] | ” |
[editar] Demonstrações
O teorema de Pitágoras já teve muitas demonstrações publicadas. O livro The Pythagorean Proposition, de Elisha Scott Loomis, por exemplo, contém 370 demonstrações diferentes.[7] Há uma demonstração no livro Os Elementos, de Euclides.[8] E também ofereceram demonstrações, o matemático indiano Bhaskara Akaria, o polímata italiano Leonardo da Vinci, e o vigésimo presidente dos Estados Unidos, James A. Garfield.[9][10][11] O teorema de Pitágoras é tanto uma afirmação a respeito de áreas quanto a respeito de comprimentos, algumas provas do teorema são baseadas em uma dessas interpretações, e outras provas são baseadas na outra interpretação.[editar] Por comparação de áreas
Não se sabe ao certo qual seria a demonstração utilizada por Pitágoras, entretanto, muitos autores concordam que ela teria sido feita através da comparação de áreas[carece de fontes], conforme se segue:- Desenha-se um quadrado de lado b + a;
- Traçam-se dois segmentos paralelos aos lados do quadrado;
- Divide-se cada um destes dois retângulos em dois triângulos retos, traçando as diagonais. Chama-se c o comprimento de cada diagonal;
- A área da região formada ao retirar os quatro triângulos retos é igual a b2 + a2;
- Desenha-se agora o mesmo quadrado de lado b + a, mas colocamos os quatro triângulos retos noutra posição.
- A área da região formada quando se retiram os quatro triângulos retos é igual a c2.
[editar] Por semelhança de triângulos

Demonstração que utiliza o conceito de semelhança: os triângulos ABC, ACH e CBH têm a mesma forma, diferindo apenas pelas suas posições e tamanhos.
Sendo ABC um triângulo retângulo, com o ângulo reto localizado em C, como mostrado na figura. Desenha-se a altura com origem no ponto C, e chama-se H sua intersecção com o lado AB. O ponto H divide o comprimento da hipotenusa, c, nas partes d e e. O novo triângulo, ACH, é semelhante ao triângulo ABC, pois ambos tem um ângulo reto, e eles compartilham o ângulo em A, significando que o terceiro ângulo é o mesmo em ambos os triângulos também,[12] marcado como θ na figura. Seguindo-se um raciocínio parecido, percebe-se que o triângulo CBH também é semelhante à ABC. A semelhança dos triângulos leva à igualdade das razões dos lados correspondentes:
Estas relações podem ser escritas como:
[editar] Demonstração algébrica
A análise da figura da direita permite computar a área do quadrado construído sobre a hipotenusa de um triângulo retângulo: ela é quatro vezes a área desse triângulo mais a área do quadrado restante, de lado (b−a). Equacionando-se, segue que: (o termo (b-a)² é um produto notável)
(o termo (b-a)² é um produto notável) (por comutatividade da multiplicação: 2ab = 2ba)
(por comutatividade da multiplicação: 2ab = 2ba)
[editar] Por cálculo diferencial
Pode-se chegar ao teorema de Pitágoras pelo estudo de como mudanças em um lado produzem mudanças na hipotenusa e usando um pouco de cálculo. É uma demonstração baseada na interpretação métrica do teorema, visto que usa comprimentos, não áreas.Como resultado da mudança da no lado a,
que resulta da adição de um segundo termo para as mudanças no lado b.
Pela integração, segue:
[editar] Pelo rearranjo das partes
Uma demonstração por rearranjo é dada pela animação à esquerda. Como a área total e as áreas dos triângulos são constantes, a área preta total é constante também. E a área preta pode ser dividida em quadrados delineados pelos lados a, b, c do triângulo, demonstrando que a2 + b2 = c2.
Na animação à direita, um grande quadrado inicial é formado da área c 2 tornando adjacentes quatro triângulos retângulos idênticos, deixando um pequeno quadrado no centro do grande quadrado, de modo a acomodar a diferença de comprimentos dos lados dos triângulos. Dois retângulos são formados, de lados a e b, movendo-se os triângulos. Incorporando o pequeno quadrado central com um destes retângulos, os dois retângulos são feitos em dois quadrados de áreas a 2 e b 2, mostrando que c 2 = a 2 + b 2.
[editar] Recíproca
A recíproca do teorema de Pitágoras também é verdadeira[14]:- "Para qualquer triângulo com lados l, m, e r, se l² + m² = r², então o ângulo entre l e m mede 90°".
| “ | Se num triângulo o quadrado em um dos lados for igual à soma dos quadrados construídos sobre os dois lados restantes do triângulo, o ângulo formado pelos dois lados restantes do triângulo é um ângulo reto. | ” |
[editar] Consequências e usos
Talvez nenhuma outra relação geométrica seja tão utilizada em matemática como o teorema de Pitágoras. Ao longo dos séculos foram sendo registrados muitos problemas curiosos, cujas resoluções têm como base este famoso teorema [carece de fontes]. É possível utilizar o teorema de Pitágoras em todos os polígonos, pois eles podem ser divididos em triângulos e esses em triângulos retângulos. E por extensão, a todos os poliedros.[editar] A diagonal do quadrado
A diagonal do quadrado divide-o em dois triângulos retângulos congruentes. Sendo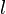 o lado e
o lado e  a diagonal, segue que:
a diagonal, segue que:[editar] A altura do triângulo equilátero
A altura do triângulo equilátero divide-o em dois triângulos retângulos congruentes. Sendo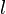 o lado e
o lado e  a altura, segue que:
a altura, segue que:[editar] Identidade trigonométrica fundamental
[editar] Ternos pitagóricos
Um terno pitagórico primitivo é aquele em que a, b e c são coprimos (o máximo divisor comum de a, b e c é 1).
Lista de ternos pitagóricos primitivos até 100:
(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)
[editar] Números irracionais como comprimento
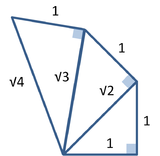
Uma das consequências do teorema de Pitágoras é que comprimentos incomensuráveis (ou seja, cuja razão é um número irracional, tal como a raiz quadrada de 2), podem ser construídos, com instrumentos como régua e compasso. Um triângulo retângulo com ambos os catetos iguais a uma unidade tem uma hipotenusa de comprimento igual a raiz quadrada de 2. A figura da direita mostra como construir segmentos de reta com comprimentos iguais a raiz quadrada de qualquer número inteiro positivo.[editar] Distância entre dois pontos
Como A e C possuem mesma ordenada,
 .
.Como B e C possuem mesma abcissa,

Então
![d(A,B)=\sqrt[]{d(A,C)^2+d(B,C)^2}=\sqrt[]{(x_1-x_2)^2+(y_1-y_2)^2}.](http://upload.wikimedia.org/math/c/7/5/c756b6f6b267e3037ec6679c8ac47d1b.png)
[editar] Generalizações
[editar] Lei dos cossenos
[editar] Teorema de Gua
[editar] Figuras semelhantes nos três lados
O teorema de Pitágoras foi generalizado por Euclides em seu livro Os Elementos para estender-se além das áreas dos quadrados nos três lados, para figuras semelhantes:[15]| “ | Erguendo-se figuras semelhantes nos lados de um triângulo retângulo, então a soma das áreas das duas menores é igual à área da maior. | ” |
[editar] Na geometria esférica e hiperbólica
O teorema de Pitágoras é derivado dos axiomas da geometria euclidiana, e de fato, a versão euclidiana não é válida nas geometrias não euclidianas. (Foi mostrado que o teorema de Pitágoras é equivalente ao postulado das paralelas) Em outras palavras, numa geometria não euclidiana, a relação entre os lados de um triângulo deve necessariamente tomar outra forma. Por exemplo, na geometria esférica, a² + b² ≠ c².Seja c a hipotenusa de um triângulo rectângulo numa geometria não euclidiana e a e b os catetos. O teorema de Pitágoras toma uma das seguintes formas:
- Na geometria esférica, tem-se
- Na geometria hiperbólica tem-se
[editar] História

O "triângulo egípcio", de medidas 3, 4, 5, os egípcios usavam uma corda com treze nós equidistantes para construírem ângulos retos.

Ilustração do livro Chou Pei Suan Ching, que sugere uma demonstração do teorema para um triângulo específico (de lados 3, 4 e 5).







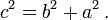

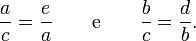

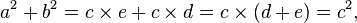


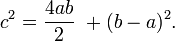


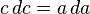






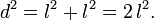



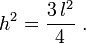

 Ver artigo principal:
Ver artigo principal: 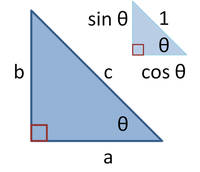

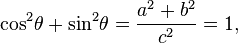





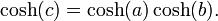

Nenhum comentário:
Postar um comentário