Os conceitos Matemáticos
1 - Sistema linear
É um conjunto de m equações lineares de n incógnitas (x1, x2, x3, ... , xn) do tipo:a11x1 + a12x2 + a13x3 + ... + a1nxn = b1a21x1 + a22x2 + a23x3 + ... + a2nxn = b2a31x1 + a32x2 + a33x3 + ... + a3nxn = b3.................................................................
.................................................................
am1x1 + am2x2 + am3x3 + ... + amnxn = bn
Exemplo:
3x + 2y - 5z = -8
4x - 3y + 2z = 4
7x + 2y - 3z = 2
0x + 0y + z = 3
Temos acima um sistema de 4 equações e 3 incógnitas (ou variáveis).
Os termos a11, a12, ... , a1n, ... , am1, am2, ..., amn são denominados coeficientes e b1, b2, ... , bn são os
termos independentes. A ênupla (a 1, a 2 , a 3 , ... , a n) será solução do sistema linear se e somente se satisfizer simultaneamente a todas as m equações.
Exemplo: O terno ordenado (2, 3, 1) é solução do sistema:
x + y + 2z = 7
3x + 2y - z = 11
x + 2z = 4
3x - y - z = 2
pois todas as equações são satisfeitas para x=2, y=3 e z=1.
Notas:1 - Dois sistemas lineares são EQUIVALENTES quando possuem as mesmas soluções.Exemplo: Os sistemas lineares
| S1: | 2x + 3y = 12 |
| 3x - 2y = 5 |
| S2: | 5x - 2y = 11 |
| 6x + y = 20 |
2 - Se um sistema de equações possuir pelo menos uma solução, dizemos que ele é POSSÍVEL ou COMPATÍVEL.
3 - Se o sistema de equações é COMPATÍVEL e possui apenas uma solução, dizemos que ele é DETERMINADO.
4 - Se o sistema de equações é COMPATÍVEL e possui mais de uma solução, dizemos que ele é INDETERMINADO.
5 - Se os termos independentes de todas as equações de um sistema linear forem todos nulos, ou seja
b1 = b2 = b3 = ... = bn = 0, dizemos que temos um sistema linear HOMOGÊNEO.
Exemplo:
x + y + 2z = 0
2x - 3y + 5z = 0
5x - 2y + z = 0
Vejamos agora os métodos para a resolução de sistema de equações:
Método da adição:
» basta eliminar uma das variáveis, através de termos opostos, recaindo numa equação do 1º grau com uma variável.
Ex: x+y=12
x-y=4
Notamos que as duas equações possuem termos opostos (y e -y). Com isso, basta somar as duas equações:
A seguir, basta substituir o valor encontrado para x em uma das equações.
8+y=12 ou 8-y=4
y=12-8 -y=4-8
y=4 y=4
O par ordenado (x,y)=(8,4) é a solução do sistema.
Método da substituição:
Consiste em eliminarmos uma das variáveis isolando seu valor numa das equações do sistema, para em seguida substitui-la na outra.
Ex: x+y=12 ... I
x-y=4 .... II
Escolhemos uma das variáveis na primeira equação, para determinarmos o seu valor: x+y=12 » x=12-y
Substituímos na outra equação:
(12-y) - y = 4
12-2y = 4
-2y = -8
y=4
Substituindo o valor encontrado em uma das equações: x+4=12 » x=12-4 » x=8
Logo a solução do sistema seria: S = {(8,4)}
Método da comparação:
Consiste em comparmos as duas equações do sistema, após termos isolado a mesma variável (x ou y) nas duas equações:
x+2y=2 » x=2-2y
x+y = 3 » x=3-y
Comparando as duas equações:
2-2y=3-y
-2y+y=3-2
-y = 1
y = -1
Substituindo o valor de y encontrado: x = 2-2.(-1) » x=2+2=4
Portando S= {(4,-1)}
Método de Kramer
No nosso exemplo , dada a equação :
Foi utilizado o método de Kramer e nele as soluções serão dadas por:
| x = (c * e - b * f ) / (a * e - b * d) y = (a * f - e * d) / (a * e - b * d) |
A interface com o usuário
Inicie um novo projeto no VB e no formulário padrão insira os controles conforme layout abaixo:
 | - temos aqui : - 6 caixas de texto - dois botões de comando - três frames |
Como você acabou de observar a interface é simples: O usuário deverá informar o valor dos coeficientes da equação nas caixas de texto e clicar no botão - Resolver - para obter o resultado da equação.
O código
Vamos começar com o código do botão - Resolver : Aplica a regra de Kramer para resolver o sistema.
Private Sub CmdResolver_Click()
On Error GoTo Err_CmdResolver_Click
Dim i%
For i = 0 To 1
AjustaValor txta(i)
AjustaValor txtb(i)
AjustaValor txtc(i)
Next
Dim valx#
Dim valy#
Dim tmp%
Dim mul0#
Dim mul1#
mul0 = Val(txtb(1))
mul1 = Val(txtb(0))
mul0 = IIf(mul0 < 0 Eqv mul1 < 0, -mul0, mul0)
valx =(Val(txtc(0)) * mul0 + Val(txtc(1)) * mul1) / (Val(txta(0)) * mul0 + Val(txta(1))*mul1)
valy =(Val(txtc(0)) - Val(txta(0)) * valx) / Val(txtb(0))
lblx = "x = " & valx
lbly = "y = " & valy
lblfraz = "A solução para o sistema é => (" & valx & " ; " & valy & ")"
Exit Sub
Err_CmdResolver_Click:
lblx = ""
lbly = ""
lblfraz = "Erro n° " & Err & " - " & Err.Description
Select Case Err
Case 6
lblfraz = lblfraz & " : ocorreu um estouro da pilha do sistema."
Case 11
lblfraz = lblfraz & " : não há solução para o sistema."
End Select
End Sub |
Abaixo o código associado a evento KeyPress de cada caixa de texto , onde só permitimos a entrada valores numéricos:
Private Sub txta_KeyPress(Index As Integer, KeyAscii As Integer)
If KeyAscii = 8 Then
txta(Index).Text = Left(txta(Index).Text, Len(txta(Index).Text) - 1)
SendKeys "{END}"
End If
'so permite valores numericos
If KeyAscii < 45 Or KeyAscii > 57 Then KeyAscii = 0
End SubPrivate Sub txtb_KeyPress(Index As Integer, KeyAscii As Integer)
If KeyAscii = 8 Then
txtb(Index).Text = Left(txtb(Index).Text, Len(txtb(Index)) - 1)
SendKeys "{END}"
End If
'so permite valores numericos
If KeyAscii < 45 Or KeyAscii > 57 Then KeyAscii = 0
End SubPrivate Sub txtc_KeyPress(Index As Integer, KeyAscii As Integer)
If KeyAscii = 8 Then
txtc(Index).Text = Left(txtc(Index).Text, Len(txtc(Index)) - 1)
SendKeys "{END}"
End If
'so permite valores numericos
If KeyAscii < 45 Or KeyAscii > 57 Then KeyAscii = 0
End Sub
|
O código associado ao botão - Novo Cálculo - que limpa todos os controles do formulário:
Private Sub limpa_controles()
Dim i As Integer
'limpa as caixas de texto
For i = 0 To Me.Controls.Count - 1
If TypeOf Me.Controls(i) Is TextBox Then
Me.Controls(i).Text = ""
End If
Next
lblfraz = ""
lblx = ""
lbly = ""
End Sub |
Para encerra o código que simula a pressionamento da tecla TAB quando o usuário tecla ENTER. Para que o código funcione você deve definir a propriedade KeyPreview do formulário como True:
Private Sub Form_KeyPress(KeyAscii As Integer) 'Esse código permite a mudança de quadro de texto através do Enter If KeyAscii = 13 Then 'Se o tipo do controle ativo for TextBox If TypeOf Screen.ActiveControl Is TextBox Then 'Simula o pressionamento da tecla TAB SendKeys "{tab}" 'A linha a seguir evita ouvir um bip KeyAscii = 0 End If End If End Sub |
Agora vou mostrar um exemplo , exibindo a tela obtida na resolução de um sistema:
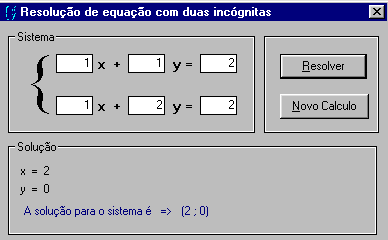
| Nota: O operador Eqv foi usado na linha de código : mul0 = IIf(mul0 < 0 Eqv mul1 < 0, -mul0, mul0) Ele é usado para efetuar uma equivalência lógica entre duas expressões. Sua sintaxe é : resultado = expressão1 Eqv expressão2
|
A interface com o usuário

Nenhum comentário:
Postar um comentário